Retour vers livre ouvert

A).Historique du nombre d'or

B).Caractéristiques mathématiques

C).Constructions géométriques et architectures

[II].LE NOMBRE D'OR CHEZ LES VEGETAUX

A).La croissance des plantes et Fibonacci

B).Disposition des feuilles sur une tige

C).Quelques plantes ou l'on retrouve phi...

[III].LE NOMBRE D'OR CHEZ LES ANIMAUX

A).Quelques animaux qui ne sont pas étrangés à phi

B).Croissance d'une population ?

C).Et chez l'homme ?

[-].CONCLUSION.

[-].BIBLIOGRAPHIE.

I.Un rapport bien particulier

--- --- --- --- --- --- --- --- ---

[A.Historique - B. Caractéristiques mathématiques - C.Géométrie et architecture -

--- --- --- --- --- --- --- --- --- --- --- ---

C).Constructions géométriques et architecture

Le Parthénon d'Athènes, que nous avons évoqué au début de cette partie, fait apparaître le nombre d’or à plusieurs reprises .

parthenon

Le Parthénon s'inscrit dans un rectangle doré, c'est-à-dire tel que le rapport de la longueur à la hauteur est égal au nombre d'or.
Sur la figure : DC/DE = phi .

Sur la toiture du temple, GF/GI = phi .

Voyons de plus près la construction d’un rectangle d’or…

Le rectangle d'or.

Un rectangle d'or est un rectangle dont le rapport longueur sur largeur est égal au nombre phi .
On part d'un côté de longueur 1/2 pour construire un triangle rectangle dont les côtés de l'angle droit mesurent 1 et 1/2.
En utilisant le théorème de Pythagore, l'hypoténuse mesure :

( 1 +√5) / 2 = phi .

Il suffit de terminer le rectangle d'or dont les côtés mesurent 1 et phi .
Le rapport de leurs longueurs est égal au nombre d'or et le rectangle est dit d’or. Ce rectangle est harmonieux, son équilibre flatte l’œil et statistiquement il a la préférence lorsqu'on le compare à d'autres rectangles de formes diverses.

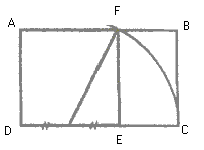
carredor

A partir de ce rectangle d’or ABCD on à tracer un nouveau rectangle d’or FBCE…

carredor

Puis un autre HGCE, et encore un nouveau IJEH et ainsi de suite …

Pourquoi une suite de rectangles d'or ?

Le premier rectangle a des côtés de longueur
1 et phi dont le rapport est phi
Le deuxième rectangle a des côtés de longueur phi - 1 et 1 soit
1/ phi et 1 dont le rapport est phi .
Le troisième rectangle a des côtés de longueur 1 - 1/ phi = 1/ phi ²,soit
1/ phi ² et 1/ phi dont le rapport est phi .
Le quatrième rectangle a des côtés de longueur 1/ phi - 1/ phi ² = 1/ phi ³ et 1/ phi ², soit 1/ phi ³ et 1/ phi ² dont le rapport est phi .
...
Le n^ième rectangle a des côtés de longueur
1/ phi ^n-3 - 1/ phi ^n-2= ( phi - 1)/ phi ^n-2 = (1/ phi )/ phi ^n-2= phi 1/ phi ^n-1
et 1/ phi ^n-2, soit 1/ phi ^n-1 et 1/ phi ^n-2 dont le rapport est phi
Nous avons donc bien une suite de rectangles d'or.

Pour arriver à une spirale … d’or bien sûr !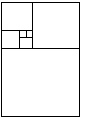

Au bout d’ un certain temps, en répétant plusieurs fois l’opération, on obtient une figure ressemblant a cela.

L’ on peut ainsi tracer la spirale d’or qui nous sera très utile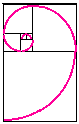

NB : cette spirale est une 'fausse' spirale parce qu'elle est constituée d'arcs de cercles au lieu d'avoir une variation continue du rayon. Cependant les raccordements des arcs sont parfaits car la condition de tangence est respectée. Les centres des arcs sont à chaque fois situés sur la même droite perpendiculaire à cette tangente. Cette courbe est connue sous le nom de 'spirale logarithmique'. Elle s'enfonce sans fin et tend rapidement vers un point Z autour duquel elle s'enroule de plus en plus près. Ce point est appelé le centre de la spirale. Appelée spirale de Bernoulli, elle a de nombreuses propriétés. L'une d'elles est que le segment de droite qui joint le centre Z à un point de la courbe croît en progression géométrique. La longueur du rayon vecteur est multipliée par le nombre d'or chaque fois que sa direction tourne d'un quart de tour. Par contre l'angle que fait ce segment avec une direction de départ quelconque, croît en progression arithmétique.

On retrouve cette spirale chez l’homme par exemple, ou chez le nautile que l’on verra dans la partie III.

Le triangle d’or.

Un triangle d'or est un triangle isocèle dont les longueurs des côtés sont dans le rapport du nombre d'or.

triangledor

Leurs angles mesurent 36 ° et 72°.

Pentagone régulier et nombre d’or.

pentagone

Le pentagone régulier est une figure d'or car la proportion entre une diagonale et un côté est le nombre d'or.

AC/AD = phi

Les triangles d’or et le pentagone régulier :

pentagone

Dans le pentagone régulier ci-contre, le triangle ABC et le triangle ACD sont tous deux des triangles isocèles dont les longueurs des côtés sont dans le rapport du nombre d'or : ce sont deux triangles d'or.

On les retrouve aussi bien dans la faune que dans la flore. Parmi les constructions vues au cours de cette partie, il y en a deux type qui apparaissent souvent (par rapport aux autres constructions du moins) : il s’agit du pentagone régulier et de la spirale d’or. La suite de Fibonacci qui a un lien direct avec j est aussi à retenir, car on la verra elle aussi un peu partout.

Maintenant, voyons si l’on retrouve bien le nombre d’or dans la nature, chez les plantes tout d’abord, puis chez les animaux (Homme compris bien sûr…).

dodecametre

Le dodécaèdre régulier dessiné par Léonard de Vinci,
un solide de 12 faces ayant pour chacune d’entre elles un pentagone régulier.

<= page précédente --- page suivante =>

***