Retour vers livre ouvert

[-].ACCUEIL.

[-].INTRODUCTION.

[I]. LE NOMBRE D'OR : LA DIVINE PROPORTION

A).Historique du nombre d'or

B).Caractéristiques mathématiques

C).Constructions géométriques et architectures

A).La croissance des plantes et Fibonacci

B).Disposition des feuilles sur une tige

C).Quelques plantes ou l'on retrouve phi...

A).Quelques animaux qui ne sont pas étrangés à phi

B).Croissance d'une population ?

C).Et chez l'homme ?

B).Modélisation de la croissance d'une population

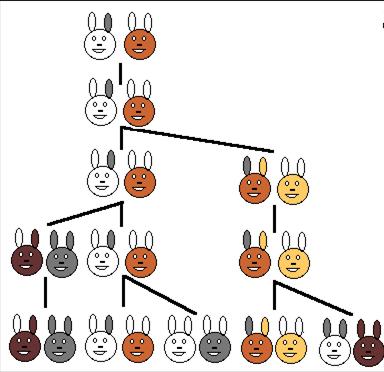
La suite de Fibonacci apparaît aux endroits les plus inattendus : comme par exemple la croissance d’une population de lapin. Léonard de Pise ( dit Fibonacci ) lui même propose dans son Liber abaci ce petit casse tête :

« Un couple de Lapins, né le 1^er janvier, donne naissance à un autre couple de Lapins chaque mois, dès qu’il a atteint l’âge de deux mois. Les nouveaux couples suivent la même loi de reproduction. Combien aura t-il de Lapins le 1er janvier de l’année suivante en supposant qu’aucun couples n’ait disparu entre temps ? »

 On note A1 le nombre de couples au départ ( c’est à dire A1=1 ) et An le nombre de lapins au nième mois.

D’après ce graphique, on a A0=0 A1=1 A2=1 A3=2 A4=3 A5=5

Donc le nombre de couples au mois n est égal à la somme du nombre de couples au mois n-1  et du nombre de couple au mois n-2.

C’est à dire An=An-1+An-2 pour n ³2

L’on remarque donc que la croissance d’une population de lapin dans des conditions idéales serait une croissance suivant la suite de Fibonacci. Elle aurait donc un rapport direct avec le nombre d’or.

Mais pour répondre à Fibonacci, au douzième mois la population de lapins sera égale à A12 (en effet décembre est le douzième mois). Mais plutôt que de calculer A7, A8,A9,A10…., essayons plutôt de trouver la formule explicite de la suite An.

Comme pour cette suite ( celle de Fibonacci ) on a An+1/An »   à partir de An  = 8. Nous savons que la suite de Fibonacci est une suite géométrique de raison  = (1+√5)/2.

 Alors à partir de An = 8 c’est à dire n=6, on peut écrire :

An = A6 ´ ((1+√5)/2)^(n-6)

Alors A12 = A6 ´ ((1+√5)/2)^(12-6)

A12 = 8 ´ ((1+√5)/2)^6

A12 = 144

Au douzième mois, il y a donc 144 couples de lapins, soit 288 lapins !

On retrouve ce genre de suite dans la croissance de la population d’autres êtres vivants, tel que les abeilles par exemple.

En réalité, une population de lapin ne suit pas aussi strictement cette règle… des lapins sont polygames, certains meurent plus tôt etc…

Affichage optimisé 800x600 & 1024x768. Site testé sous Internet Explorer 6, Mozilla et Konqueror. TPE L'araignée et sa toile - 2004